Spotkanie 1. * 15.09.2023 * 13:00 - 15:00

• Podstawowe funkcje cube(), cylinder() i sphere() i bryły przez nie wyranedrowane.
• Tajemnicza zmienna $fn i efekty jej stosowania.
• Figury płaskie (2D) – funkcje square() i circle() oraz funkcja linear_extrude() (wyciągnięcie liniowe).

Sześcian // 1. Sześcian o krawędzi 50 mm a = 50; cube(a); // 2. Sześcian o krawędzi 50 mm a = 50; cube([a, a, a]); // 3. Sześcian o krawędzi 50 mm a = 50; linear_extrude(a) square(a);
	Prostopadłościan // 1. Prostopadłościan o krawędziach 30, // 40 i 50 mm cube([30, 40, 50]); // 2. Prostopadłościan o krawędziach 30, // 40 i 50 mm a = 30; b = 40; c = 50; cube([a, b, c]); // 3. Prostopadłościan o krawędziach 30, // 40 i 50 mm a = 30; b = 40; c = 50; linear_extrude(c) square([a, b]);
Walec // 1. Walec o wysokości 50 mm i promieniu 20 mm cylinder(h = 50, r = 20); // 2. Walec o wysokości 50 mm i promieniu 20 mm h = 50; r = 20; cylinder(h, r, r); // 3. Walec o wysokości 50 mm i promieniu 20 mm h = 50; r = 20; linear_extrude(h) circle(r);
	Walec, stożek ścięty i stożek oraz przesunięcie równoległe // Walec o wysokości 50 mm i promieniu 20 mm cylinder(50, 20, 20); /* Stożek ścięty o wysokości 50 mm i promieniach podstaw 20 i 10 mm */ translate([50, 0, 0]) cylinder(50, 20, 10); /* Stożek o wysokości 50 mm i promieniu podstawy 20 mm */ translate([100, 0, 0]) cylinder(50, 20, 0);
Walec z parametrm $fn i graniastosłupy oraz przesunięcie równoległe // Graniastosłup trójkątny prawidłowy cylinder(50, 20, 20, $fn = 3); // Graniastosłup czworokątny prawidłowy translate([50, 0, 0]) cylinder(50, 20, 20, $fn = 4); // Graniastosłup sześciokątny prawidłowy translate([100, 0, 0]) cylinder(50, 20, 20, $fn = 6);
	Walec z parametrm $fn i ostrosłupy oraz przesunięcie równoległe // Ostrosłup trójkątny prawidłowy cylinder(50, 20, 0, $fn = 3); // Ostrosłup czworokątny prawidłowy translate([50, 0, 0]) cylinder(50, 20, 0, $fn = 4); // Ostrosłup pięciokątny prawidłowy translate([100, 0, 0]) cylinder(50, 20, 0, $fn = 5);
Kula i kula z parametrm $fn sphere(20); translate([50, 0, 0]) sphere(20, $fn = 4); translate([100, 0, 0]) sphere(20, $fn = 10);
	Pionek – suma trzech brył // domyślna wartość parametru $fn difference(){ // podstawa - od kuli ... sphere(25); // odejmujemy dwa prostopadłościany translate([0, 0, -12.5]) cube([50, 50, 25], center=true); translate([0, 0, 25]) cube([50, 50, 25], center=true); } cylinder(50, 20, 10); // kolumna - stożek ścięty translate([0, 0, 50]) sphere(15); // kula na wierzchołku
Pionek z parametrm $fn = 300 $fn = 300; // długi czas randerowania difference(){ sphere(25); translate([0, 0, -12.5]) cube([50, 50, 25], center=true); translate([0, 0, 25]) cube([50, 50, 25], center=true); } cylinder(50, 20, 10); translate([0, 0, 50]) sphere(15);

Spotkanie 2. * 22.09.2023 * 13:00 - 15:00

Zbudowane za pomocą różnych funkcji bryły w naturalny sposób łączą się ze sobą. Można również zastosować kilka funkcji do wykonania do operacji na bryłach:

• Funkcja union() – łączenie brył (suma zbiorów) .
• Funkcja intersection() – część wspólna brył (iloczyn, przecięcie zbiorów).
• Funkcja difference() – różnica brył (różnica zbiorów).

Bryły obrotowe można budować przez obrót figury płaskiej dookoła osi OX. Obracana figura musi znajdować się w po jednej stronie osi OX w płasczyźnie XOY. Funkcja rotate_extrude() randeruje bryłę obrotową i następnie ustawia ją w przestrzeni tak, jakaby oś OZ była osią obrotu (ptzykład: torus).

Suma sześcianu i kuli $fn = 128; // naturalne łączenie kolejnych obiektów cube(50, center = true); sphere(33); $fn = 128; // zastosowanie funkcji union() union() { cube(50, center = true); sphere(33); }
	Różnica sześcianu i kuli $fn = 128; difference() { cube(50, center = true); sphere(33); }
Część wspólna sześcianu i kuli $fn = 128; intersection() { cube(50, center = true); sphere(33); }
	Bryły obrotowe - Torus $fn = 128; rotate_extrude() translate([50, 0, 0]) circle(25);

Spotkanie 3. * 06.10.2023 * 9:00 - 12:00 * Podsumowanie i wystawa prac uczestników wydarzenia.

Czworościan foremny (1)

	/* 
	 * Czworościan foremny - jedna z pięciu brył platońskich
	 */

	a = 100;                // długość krawędzi czworościanu
	R = a * sqrt(3) / 3;    // promień okręgu opisanego na podstawie
	H = a * sqrt(6) / 4;    // wysokość czworościanu foremnego

	cylinder(H, R, 0, $fn = 3);
	

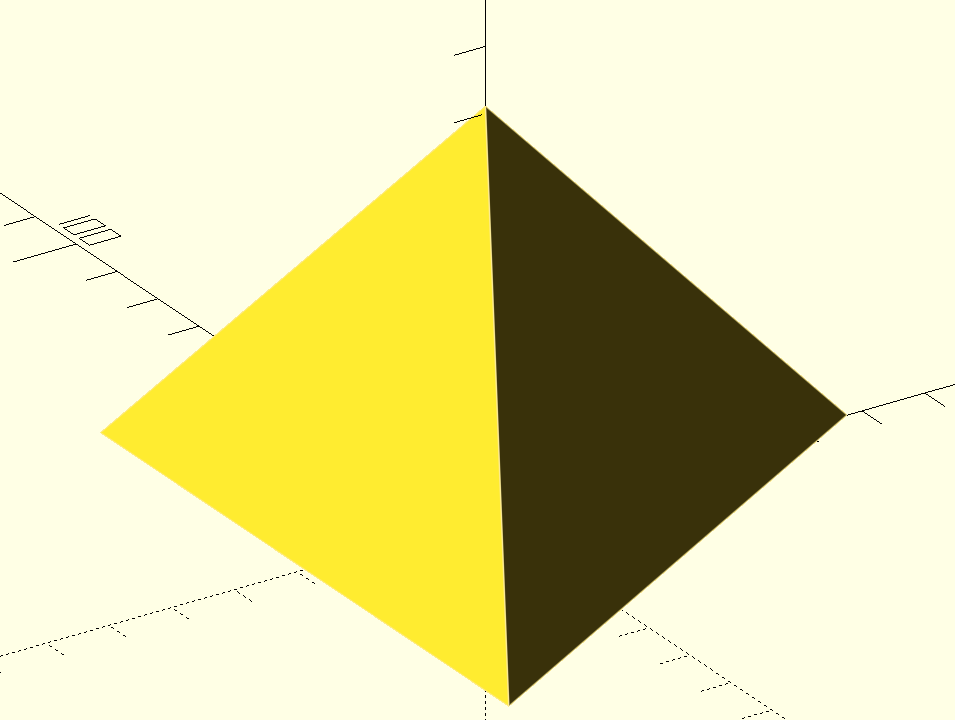
Czworościan foremny (2)

	a = 100;         // długość krawędzi sześcianu
	d = a * sqrt(2); // przekątna ściany sześcianu - krawędź czworościanu
	points = [ // wierzchołki czworościanu foremnego
	    [-d/2, 0, 0], [d/2, 0, 0], [0, -d/2, a], [0, d/2, a]
	];

	faces = [ // ściany czworościanu
	    [1, 0, 2], [0, 1, 3], [2, 3, 0], [3, 2, 1]
	];
	
	polyhedron(points, faces);
	

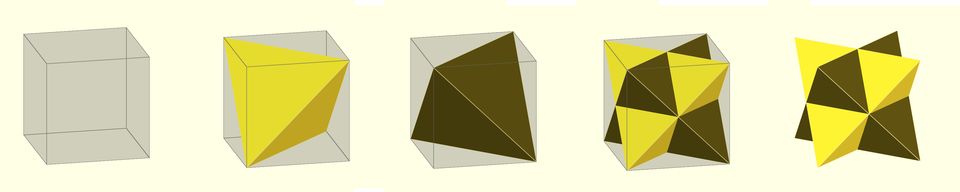
Czworościan foremny, obrót i stella octangula

	a = 100;         // długość krawędzi sześcianu
	d = a * sqrt(2); // przekątna ściany sześcianu - krawędź czworościanu
	points = [[-d/2, 0, 0], [d/2, 0, 0], [0, -d/2, a], [0, d/2, a]];
	faces = [[1, 0, 2], [0, 1, 3], [2, 3, 0], [3, 2, 1]];
	
	polyhedron(points, faces);
	rotate([0, 0, 90]) polyhedron(points, faces);
	color("black", 0.1) cylinder(a, d=d, $fn = 4); // sześcian
	

GALERIA ZDJĘĆ